▣ 상관 계수

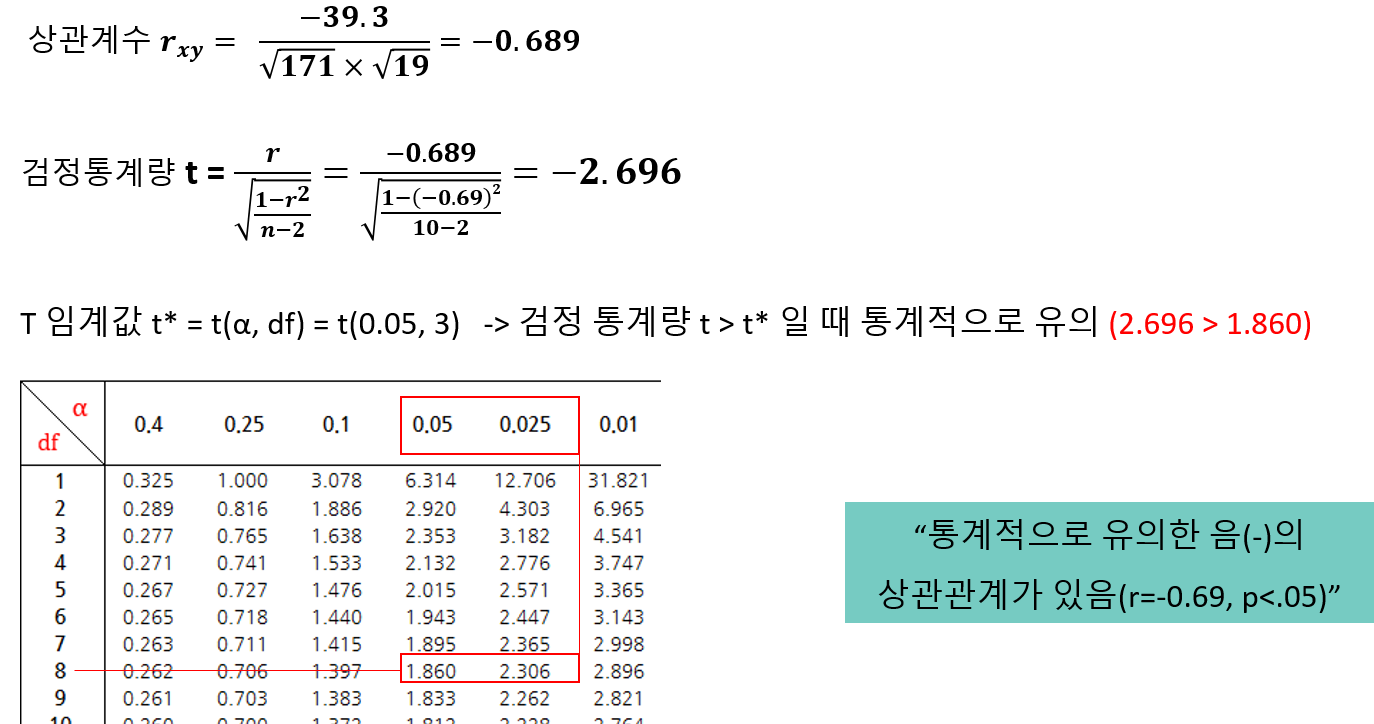
▣ 피어슨 상관관계
● 두 변수(간격, 비율척도) 간 선형 관계(방향, 크기)를 추정
● 전제조건
∨ 독립성: 표본들은 확률적, 독립적으로 추출
∨ 정규성: 변수들은 모두 계량적이고 정규분포(중심극한정리에 의해 표본수 30이상 가능)
∨ 충족이 안되면 자료 변환(로그 등)
● 부적합한 상관분석

비선형은 선형성의 전제조건에 위배되고, 이상값은 X 상관계수에 영향을 주어서 분석결과를 신뢰할 수 없다. 고정간격은 X값이 미리 일정한 간격으로 정해지면 안된다. 예를 들면 학년별 성적(1~4학년)과 성적 간 관계에서 학년은 고정된 간격의 값이라 이산변수가 되기 때문에 피어슨 상관분석은 안된다. 상이한 집단에서 측정한 값은 집단간 이질성으로 인해 자료의 분산이 커지게 되고 편향된(bias) 표본자료로 신뢰할 수 없다.
● 분석 – 상관분석 – 이변량 상관(상관계수: pearson / 옵션: 평균과 표준편차)


▣ 스피어만 상관관계
● 순서형 두 변수의 선형관계를 추정하기 위한 비모수적 통계검정
● 서열척도 혹은 정규성을 만족하지 않는 계량자료의 상관분석 이용
● 표본수가 적고 정규분포를 가정할 수 없는(n<30) 연속형 자료 포함
● 피어슨의 상관계수와 식의 형태는 같지만 데이터의 실제 값 대신 순위(rank)를 이용

∨ ri= x1,……xn에서 xi의 순위, R=(r1, r2……rn) / si= y1,…….yn에서 yi의 순위, S-(s1, s2……sn)
● 짝지어진 두 변수(x, y)를 각각 순위를 매긴 후 그 순위의 차를 통해 검정


비율척도로 구성된 자료를 굳이 서열척도로 구분하는 스피어만 상관분석을 사용할 필요가 없다. 물론 정규성 가정이나 표본수가 30미만이라면 사용해야겠지만, 그렇지 않다면 피어슨상관분석을 하는 것이 바람직하다. 실제 많은 연구에서 스피어만 상관계수는 제한된 상황에서만 사용하고 그렇게 많이 이용되지 않는다.
● 분석 – 상관분석 – 이변량 상관(상관계수: spearman, Kendall)

비모수 상관분석에서는 데이터 본래의 값이 모두 제거되고 순위 정보만이 분석에 이용되므로 두 변수 간의 선형적 연관성을 추정할 수 있는 것은 아니다. 때문에 비모수 상관분석은 두 변수의 선형성이 아니라 한 변수가 증가할 때 다른 변수도 증가하는 경향이 있느냐 하는 상관성이다.

▣ 결정 계수(r2)
● 결정계수 r2은 두 변수 간 선형관계의 정도를 설명하는 설명력(회귀분석의 r2)
● 상관 계수와 연관된 개념으로 두 변수 간 공통 분산의 비율을 의미하고, 종속변수의 총 분산에 대한 독립변수에 의해 설명된 분산
∨ r = 0.7 이라면, 한 변수의 전체 분산의 49%를 다른 변수가 설명함을 의미(r2=0.49)
∨ 즉, 상관계수가 0.7이라면 변수 간 49% 만큼 설명이 가능함을 의미

상관관계 구하는 방법 논문통계강의로 확인하세요▼▼▼
"논문의 품질을 높이는 열쇠!!!
퀵데이터 논문통계분석을 통해 더욱 탄탄한 논문을 완성하세요."
퀵데이터 논문컨설팅은 논문 주제 선정부터, 연구모형, 통계분석, 심사 준비까지 전문 지도 박사님의 1:1 맞춤형 컨설팅 통해 효율적이고 빠른 논문작성을 도와드립니다. 논문 검토, 논문편집, 논문 통계분석까지 직접적인 컨설팅을 원한다면 퀵테이터에 문의하세요 상담문의 1600-7473
'논문자료 > 논문통계분석' 카테고리의 다른 글
| [논문통계분석] 편상관관계 분석 및 해석하는 방법 완벽이해하기, 편상관관계분석 강의_퀵데이터 (0) | 2024.07.17 |
|---|---|
| [논문통계분석] 편상관관계 개념 이해, 허위상관이란?, 논문통계분석 강의 (0) | 2024.07.16 |
| [논문통계분석]상관분석 개념 및 상관계수 구하는 방법, spss 상관분석, 통계분석강의 (0) | 2024.07.04 |
| [논문통계분석] 논문 신뢰도 높이는 방법, spss논문통계, 크롬바하알파값, 신뢰도분석_논문통계강의 (0) | 2024.06.05 |
| [논문통계분석] 논문에서 사용되는 반복측정분산분석(RM_ANOVA) spss분석방법 및 해석 방법 _통계분석강의_퀵데이터 (0) | 2024.04.29 |





