로지스틱 회귀분석은 19세기 퀘틀레(Quetelet)와 베르헐스트(Verhulst)가 인구증가에 대한 연구를 하면서부터 시작되었다. 인구증가가 최초에는 지수적 증가에 의한다고 생각되었는데 나중에는 불가능한 수에 도달하게 되면서 이를 보완하기 위한 통계적 모형으로 로지스틱 함수가 이용되었다. 1938년에 피셔(Fisher)와 예이츠(Yates)가 이항 결과변수를 분석할 때 logit 변환에 의한 회귀모형을 제시하였다.
◈ 이항로지스틱 회귀분석 통계분석방법 및 해석
📌 연구문제

📌 분석 방법 : SPSS 프로그램-분석-이분형 로지스틱


❶ 이분형 종속변수의 코딩값이 자료분석을 위해 변환된 값(1=0, 2=1로 자동변환)
❷ 모든 케이스들을 더 큰 집단에 분류하여 정확도는 항상 50%이상, 본 예제에서 분석의 분류 정확도는 63.8%

❸ 0단계는 로지스틱 회귀분석의 첫 단계 모형을 의미하고, 이 단계는 독립변수 없이 상수항으로만 구성됨
❹ 로지스틱 회귀분석에 포함되지 않은 4개의 독립변수의 유의성으로 모든 변수가 유의함

모형계수의 총괄검정 결과표에 카이제곱 유의확률을 보면, 독립변수가 투입되지 않았을 때와 비교해서 –2로그 우도가 유의한 수준으로 감소했는지를 의미하는 값이다.
• 1단계는 최종 모형을 의미, 상수항만으로 구성된 모형과 독립변수들이 포함된 모형의 적합도 차이의 유의성을 검증한 결과
• 포함된 독립변수들의 계수가 0이라는 귀무가설을 검증
• X제곱=47.202, p=.000으로 귀무가설 기각(H0: 모형은 유용하지 않다) 즉, 독립변수의 영향력이 0이라고 할 수 없어 모형은 유용하다
• 4개의 독립변수는 결합적으로 취업추천을 구분하는데 유용하다

• -2로그 우도(-2 log likelihood: -2LL)는 모형의 적합도를 나타냄
• 분석은 314.214로 나타남(-2LL이 낮을수록 적합도가 높고, -2LL이 0인 경우 적합도는 완벽함)
• Cox와 Snell의 R제곱과 Nagelkerke R제곱은 회귀분석의 R제곱 개념
• 결과 종속변수 분산의 15.7%~21.5%가 모형에 의해 설명됨
-2로그 우도는 모형의 적합도를 판단하는 데 기준이 명확히 정해진 것은 아닌데 값이 적을수록 양호하다고 판단한다. 우도의 로그값에 -2배 한 지표를 추정된 모델이 데이터를 얼마나 잘 적합시키는지 척도로 사용한다. 잘 적합된 모델일수록 관측값의 우도는 증가하게 되고, 우도값이 증가할수록 -2LL 값은 작아진다. 즉, 잘 적합된 모델일수록 –2LL값은 작아진다.
컥스와 스넬의 R제곱과 네겔커크 R제곱은 유사 R제곱이라고 하는데 모형의 설명력이다. 종속변수가 범주형 자료라서 일반 회귀분석보다는 설명력이 다소 낮게 나타는게 일반적이다. 그래서 모형의 적합성 강도를 판단할 수 있으나 선형회귀에 비해서는 잘 사용되지는 않는다.

• Hosmer와 Lemeshow 검정의 카이제곱 값은 회귀모형의 또 다른 적합도
• 종속변수의 실제치와 모형에 의한 예측치 간의 일치 정도로 값이 작을수록 모형의 적합도는 높음
• 분석에서 X2=5.886, p=.66으로 유의하지 않아서 실제치와 예측치는 일치한다는 귀무가설을 기각하지 않아 모형의 적합도는 충족됨
호스모와 램쇼 검정은 예측치와 실제치 사이에 유의한 차이가 있는가 검증하는 것이다. 전체 케이스를 일정한 케이스 크기로 순서대로 나눠서 실제 관측 빈도와 예측 빈도를 비교하는 분할표에 근거해서 로지스틱 회귀모형의 예측 적합도를 검정하는 방법이다. 예측치가 실제치와 비슷해야 예측이 잘 되었다고 할 수 있는데 유의확률이 0.05 이상이면 예측치와 실제치 간에 차이가 없다고 판단할 수 있다. 쉽게 이 검정은 무조건 유의확률 0.05보다 크게 나와야 한다.

분류표는 관측치와 예측치를 비교해서 어느정도 예측이 가능한지의 정확도를 나타낸다.
• 취업 추천 안함 집단에 소속된 176명 중 154명이 제대로 분류됨
• 취업 추천함 집단에 소속된 100명 중 40명이 제대로 분류되었음을 나타냄
• 전체 분류 정확도는 70.3%

B값이 0보다 크면 독립변수가 증가할 때 종속변수가 발생할 가능성이 커지고, 0보다 작으면 발생 가능성이 작아진다고 판단할 수 있다.
• 방정식 변수 표 중 1단계로만 나타난 것은 모든 독립변수가 한번에 분석되었음을 나타냄(분석시 입력 기본 설정)
• 회귀계수(B)가 양(+)이면 해당 변수값이 클수록 1인 집단(취업 추천함)에 분류되고, 음(-)이면 변수값이 클수록 0인 집단(취업 추천안함)에 분류됨
• 분류집단 예측력을 검증하기 위해 계수의 유의성 확인, 분석에서 직무자율성과 동료협력이 (+)으로 유의함
• 즉, 직무자율성(wald=8.978, p<.01)과 동료협력(wald=5.641, p<.05)이 취업추천을 구분하는데 유용하며 이들 값이 클수록 취업 추천하는 집단에 분류될 가능성이 크다고 판단할 수 있음
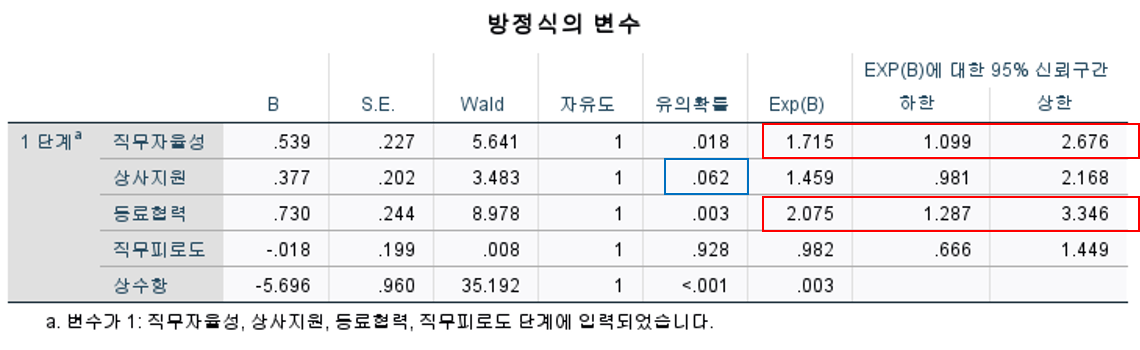
★ 유의확률은 양측검증을 전체로 산출된 값으로 가설이 방향적 가설이면 계수의 유의확률은 ½이 됨
• Eg. 연구 가설이 “상사지원이 높을수록 취업 추천을 할 것이다.“ 라면 상사지원도 유의적으로 판단할 수 있음
(p=0.062 / 2) = 0.031)
• EXP(B)는 e B 를 의미하는 것으로 odds를 나타내고, odds는 0인 집단(추천 안함)에 속할 확률 대비 1인 집단(추천함)에 속할 확률의 비율을 나타냄
• 직무자율성과 동료협력의 값이 1만큼 커지면 추천안함 집단 대비 추천함 집단에 속할 확률이 각 1.715배, 2.075배가 됨 (EXP(B)는 계수의 부호가 (+)이며 1보다 크고, (-)이면 1보다 작음)


• P(사건발생 Yes)=내부값 1로 계산된 집단
• 1-P(사건발생 No)=내부값 0으로 계산된 집단
• Odds는 로지스틱 회귀분석에서 종속변수(0~∞)
• e는 자연로그의 밑수(e1=2.718)

• X는 각 케이스의 변수에 해당하는 데이터
• (x1): 직무자율성, (x2): 상사지원, (x3): 동료협력, (x4): 직무피로도

★ 확률이 기준값(p) 0.5 이상으로 취업추천 하는 집단(Yes=1)
이항 로지스틱 회귀분석은 어떤 사건이 발생하는지 안하는지를 직접 예측하기보다는 그 사건이 발생할 확률을 예측하기 때문에 종속변수값은 0과 1사이의 값을 갖는다. 확률이 0.5보다 크면 그 사건이 일어나고, 0.5보다 작으면 그 사건이 일어나지 않는 것으로 예측하는 것이다.
케이스 1번은 응답 분류 자체부터 추천하는 집단 1로 되어있다. 식에 대입해서 보면 추천하는 집단에 소속될 확률은 약 82.4%이고, 기준값 0.5보다 크므로 추천할 집단에 소속될 것으로 예측된다. 원래 취업추천으로 응답이 되었다하더라도 오즈비의 식을 통해 다른 집단에 분류될 수도 있다. 그러나 많은 케이스를 그것도 손으로 일일이 계산할 수 없다. 그래서 분석 설정할 때 예측값 중 확률과 소속집단을 새로운 변수로 저장하도록 지정한 것이다. 새로운 변수가 생성되는데 Pre1은 추천는 집단에 분류될 예측확률이고, PGR1은 예측 집단을 의미한다. 계산식과 SPSS에서 나타난 값이 다른 것은 소수점 자리수에 따른 반올림이 반영되었기 때문에 달라지는데 큰 차이가 없다.
로지스틱 회귀분석 강의 2탄 : 이항로지스틱 회구분석 방법 및 해석▼▼▼
"논문의 품질을 높이는 열쇠!!!
퀵데이터 논문통계분석을 통해 더욱 탄탄한 논문을 완성하세요."
퀵데이터 논문컨설팅은 논문 주제 선정부터, 연구모형, 통계분석, 심사 준비까지 전문 지도 박사님의 1:1 맞춤형 컨설팅 통해 효율적이고 빠른 논문작성을 도와드립니다. 논문 검토, 논문편집, 논문 통계분석까지 직접적인 컨설팅을 원한다면 퀵테이터에 문의하세요







