
데이터가 흩어진 정보를 보여주는 지표로는 표준편차가 있습니다.
상대도수 히스토그램은 각각의 계급마다 몇 %의 데이터가 있는가에 대하여 비율을 알 수 있는 그래프입니다.
표준편차를 이용해서도 비율을 알 수 있습니다.
예를 들어 성인 남자 키가 평균 170cm, 표준편차 6cm의 데이터가 있다고 해볼게요.
이 2개의 데이터만으로도 성인 남자 키가 어떤 식으로 분포되어 있는가를 알 수 있답니다.
실제로 키는 ‘정규분포’ 형태에 매우 가까운데, 이를 사용하면 182cm인 남성은 상위 2%, 즉 100명 중 2번째라는 것을 알 수 있습니다.
이렇게 우리 실생활에는 정규분포로 볼 수 있는 예가 아주 많답니다.

*정규분포는 좌우대칭의 종모양을 하고 있습니다.
정규분포를 따르는 데이터에서는 평균값에서 표준편차 몇 개만큼 떨어져 있는지(표준점수)로 비율을 알 수 있습니다.
정규분포가 종모양으로 바뀌는 이유

위 그림은 성인 남성 키 데이터를 계급 폭 6cm의 히스토그램으로 나타낸 것입니다.
첫 번째 그림은 계급값 6cm로 정규분포 그래프처럼 되어 있죠?
두 번째 그림은 계급값 3cm로 바꾼거에요. 무엇이 변했을까요?
하나의 계급 폭에 대한 데이터의 비율이 줄어든 것이 확인되죠?
전체적으로 완만한 산 모양이 되었어요.
마지막 그림은 히스토그램의 계급 폭을 무한정 작게 만든 겁니다.
이렇게 계속 되면 정규분포와 같은 종 모양이 되는 거랍니다.
통계를 위해서는 정규분포를 꼭 이해해야 합니다!!
정규분포 없이는 통계학을 말할 수 없을 정도로 아주 중요합니다.
따라서 정규분포를 꼭 이해하려는 노력을 하셔야해요.
퀵데이터에서 정규분포를 조금이나마 더 쉽게 설명하도록 하겠습니다.
예를 들어 개인의지와 생활습관의 영향을 받는 성인의 몸무게는 정규분포를 따르지 않지만 임신 기간이 비슷한 태아의 몸무게와 유전적 영향이 큰 키 등의 데이터는 정규분포 형태를 가집니다.
자연현상에 한정되는 것 외 기업에서 생산된 제품의 길이와 무게에 대한 산포도(데이터가 흩어진 정도)도 정규분포에 가까우므로 품질관리 등에 이용할 수 있어요.
표준 정규분포표로 어떤 값이 데이터의 몇 %에 속하는지 알 수 있습니다!!
평균키(평균값: μ) =170cm, 표준편차(σ)=6cm의 정규분포

* 위 그림은 평균 170cm부터 176cm까지 남성은 전체 34.13%를 뜻하는 정규분포입니다.
키는 정규분포를 따르기 때문에 위 사진처럼 평균값에서 그 값까지인 사람이 데이터 전체의 몇 %를 차지한다
라는 것을 바로 알 수 있습니다.
그러면 정규분포에 34.13% 라는 숫자는 어떻게 나온 걸까요?
여기에서 등장하는 것이 바로 정규분포표를 사용했을 때 편리한 표준정규분포표입니다.
아래 표에 있는 Z는 표준점수(z점수)라고 생각하시면 됩니다.

표준정규분포표 보는 방법
표준정규분포표는 세로 방향이 표준점수의 소수 첫째 자리를, 가로 방향이 표준점수의 소수 둘째 자리를 나타냅니다.
키 170~176cm인 사람이 전체 데이터에서 차지하는 비율을 알려면
평균(μ) = 170cm, 표준편차(σ) = 6cm에서 176cm의 표준점수를 구해야 합니다.
표준점수는 표준편차를 나누어 얻습니다.
표준점수 = (176-170) ÷ 6 = 1
키와 표준점수를 대응시킨 것이 아래 그림입니다.

표준점수 1(1.00)을 표준정규분포표에서 보면 세로방향으로 1.0, 가로방향으로 0.00의 값은 0.3413인 것을 찾을 수 있으시죠?
따라서 표준점수 0~1인 키 170~176cm의 비율은 34.13%가 되는 것입니다.
* 표준정규분포표는 통계학 책이나, 인터넷에서 검색하면 잘 나옵니다.
표준정규분포표를 사용해 데이터 값의 비율을 구해볼게요.
평균값에서 떨어진 범위를 아래와 같이 계산하면 됩니다.
표준점수 구하는 방법_퀵데이터
https://blog.naver.com/quickdata7/221970044258
데이터가 흩어진 정도, 표준편차 사용방법은?_퀵데이터
통계학은 데이터 값이 얼마나 흩어져 있는가에 주목 일상적으로 통계와 관련하여 데이터 값의 중심(평균...
blog.naver.com
표준정규분포표로 비율을 구한다!!
한국 성인 남성의 키 데이터 평균(μ) = 170cm, 표준편차(σ) = 6cm 라고 한다면,
이러한 데이터에서 키 180~185cm가 차지하는 비율은 몇 %일까요?
1) 키 185cm의 표준점수를 구합니다.

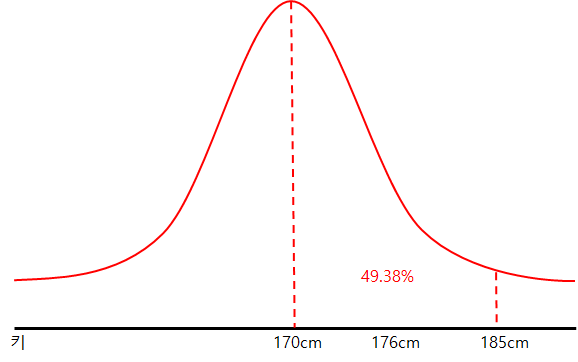
2) 키 180cm의 표준점수를 구합니다.

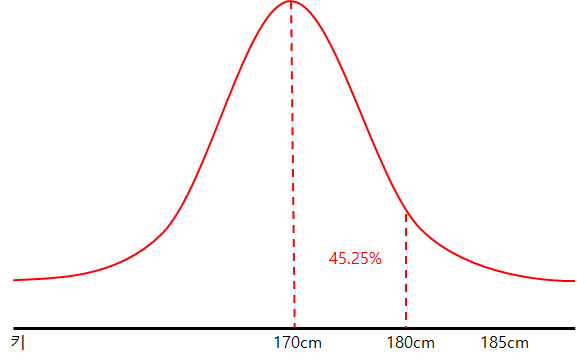
3) 1)과 2)의 평균값에서 각각의 키가 차지하는 비율을 표준정규분포표에서 찾습니다.

그 비율 간 차이를 구합니다.
49.38 - 45.25 = 4.13%
즉, 이 데이터에서 키 180~185cm의 성인 남성이 차지하는 비율을 약 4%라고 할 수 있는 것이죠.
데이터 전체에서 상위 몇 %를 차지하는지 구한다!!
한국 성인 남성의 키 데이터 평균(μ) = 170cm, 표준편차(σ) = 6cm라고 한다면,
이 데이터에서 키 190cm 이상이 차지하는 비율은 몇 % 일까요?
1) 190cm의 표준점수를 구한다.
(190-170) ÷ 6 = 20 ÷ 6 = 3.33
2) 평균값(170cm)에서 190cm까지가 차지하는 비율을 표준점수 3.33을 이용해 표준정규분포표에서 구할 수 있어요.
표준 정규분포표의 값 = 0.4996
즉, 전체에서 차지하는 비율 = 49.96%
3)평균값보다 위의 비율은 50%이므로,
50% - 49.96% = 0.04%가 됩니다.
즉, 키 190cm 이상이 차지하는 비율은 전체의 0.04%가 되는 것이죠.
이상 퀵데이터에서 통계학의 기본 정규분포에 대해 알아보았습니다~^^
#퀵데이터 #정규분포 #데이터분석 #통계분석 #기업통계 #논문통계 #논문컨설팅 #표준정규분포
'논문자료 > 논문통계분석' 카테고리의 다른 글
| 통계는 왜 필요할까요???_퀵데이터 (0) | 2020.08.18 |
|---|---|
| 통계학의 척도! 데이터 분류 기준은 어떻게 할까요?_퀵데이터 (0) | 2020.08.18 |
| 표준편차 구하는 방법 쉽게 알아보기_퀵데이터 (0) | 2020.08.18 |
| 데이터가 흩어진 정도 표준편차, 데이터 분석 기본기! 표준편차로 자료 분산 이해하기 (0) | 2020.08.18 |
| [퀵데이터] 산술평균과 기하평균 중 매출 증가율 구하는 방법은? (0) | 2020.08.18 |






