통계학은 다양한 사회 문제를 해결할 목적으로 만든 학문입니다. 통계 분석을 위해 수학의 힘을 빌리지만 통계학 수치는 어디까지나 판단 기준의 하나일 뿐입니다. 통계와 함께 경험이나 직감을 충분히 활용해 제대로 판단하는 것이 중요합니다.
데이터 간의 관계성
“두 데이터를 산포도와 상관분석으로 분석한다”
우리가 살고 있는 집의 임대료가 어떤 기준으로 정해졌을까요?
보통 건축년수, 입지, 설비, 방개수, 기타 등 요소들이 있지만 그 중에서 입지라는 요소가 아주 중요하죠.
역에서 집까지 거리가 부동산 가격에 영향을 주는 것처럼 역까지 몇 분 걸리는지가 중요합니다.
집에서 역까지 소요시간과 부동산 가격을 아래 표와 같이 예로 들어보겠습니다.
단, 기타 다른 조건은 같다고 가정합니다.
위 표를 보니 어떤 생각이 드나요?
역에서 가까워지면 집 가격은 비싸지고 멀어지면 가격은 내려갑니다. 여기서 중요한 점은 소요시간과 집 가격 간에 관계가 있을 것입니다.
관계성을 시각적으로 알기 쉽게 표현하려면 산포도를 사용하면 좋습니다.
산포도를 간단히 살펴보면 아래와 같은 그림이 되겠죠.
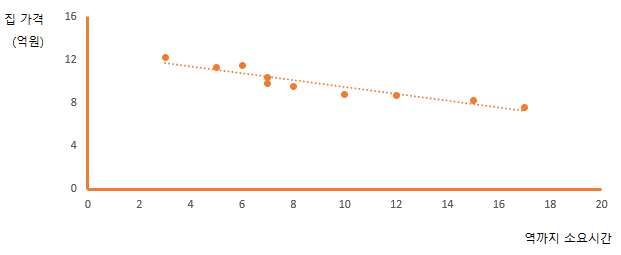
그리고 데이터가 직선임을 나타내고 있습니다. 한쪽 값이 올라가면 그것에 따라 다른 한쪽 값은 내려가는 관계를 음의 상관관계라고 합니다.
음의 상관관계가 있다면 반대로 양의 상관관계도 있습니다. 이것은 한쪽 값이 올라가면 다른 쪽 값도 올라가는 관계입니다.
이제 부터가 중요한데 직선적인 관계가 어느 정도인지를 나타내튼 지표로 상관계수 r 이 있습니다. 상관계수 값은 반드시 -1 ≤ r ≤ 1 가 됩니다. 값이 ±1에 가까울수록 직선적인 관계가 강하다고 할 수 있습니다.
상관이라는 것은 예를 들어 기온과 아이스크림 판매량의 관계라든가, 나이와 기억력의 관계라든가 등등 한쪽 값이 변하면 다른 한쪽 값도 변하는 것으로 이러한 관계는 실제로 주변에 상당히 많습니다.
두 종류 이상 데이터의 관계, 다변량 분석의 기초 상관
그러나 우리 주변에서 벌어지는 일은 대부분 여러 데이터와 연관이 있습니다. 예를 들어 건강검진을 받으면 키 뿐만 아니라 몸무게나 혈액형 등도 알 수 있죠. 이력서에는 성별, 나이 등을 쓰고 그것들을 모아 조사하면 데이터끼리의 동향과 관계성을 발견할 수 있습니다.
이때 분석 대상이 되는 데이터를 '변량(variate)'이라 하고, 키와 몸무게처럼 분석 대상이 다른 둘 이상의 데이터를 '다변량(multivariate)'이라고 합니다. 따라서 둘 이상 데이터의 관계성을 분석하는 방법을 통계학에서 '다변량분석(multivariate analysis)'라고 합니다.
전에 퀵데이터에서 한 종류의 데이터를 보는 방법으로 중심을 나타내는 값(평균값 등의 대표값)과 흩어진 정도(표준편차 등의 산포도)를 알아보았습니다.
https://blog.naver.com/quickdata7/221958702257
산술평균과 기하평균 중 매출 증가율 구하는 방법은?
일상생활에서 자주 사용하는 평균은 데이터들을 더해서 구합니다. 즉 덧셈의 합계를 데이터 수로 나눈 값...
blog.naver.com
https://blog.naver.com/quickdata7/221970044258
데이터가 흩어진 정도, 표준편차 사용방법은?_퀵데이터
통계학은 데이터 값이 얼마나 흩어져 있는가에 주목 일상적으로 통계와 관련하여 데이터 값의 중심(평균...
blog.naver.com
이번에는 두 종류 데이터의 관계성을 예로 들어 살펴보겠습니다.
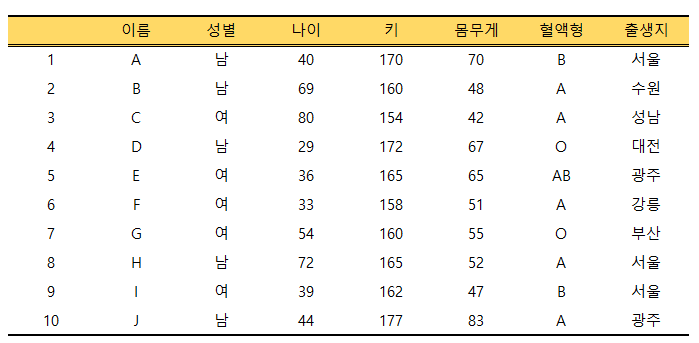
위와 같은 데이터(다변량)를 수집했다고 가정했을때 키와 나이의 관계, 성별과 출생지가 키에 영향을 줄 것인가, 혈액형은 어떨지 등등 다양한 의문이 생길겁니다.
산포도를 보면 두 데이터 간의 상관이 보인다.
앞에서 살펴본 부동산 가격 결정요인으로 역까지 소요시간의 데이터를 10건 모으고 숫자만 비교하면 역에서 가까울수록 집 가격이 비싸다는 느낌을 받습니다.
상관은 두 변량의 관계성을 가리키는 것으로 산포도는 두가지 변량을 가로축, 세로축의 그래프 위에 점을 찍어 나타낸 일종의 도표입니다.
역까지 소요시간과 집 가격이라는 두 변량을 점으로 나타낸 산포도를 보면 우하향 형태를 띄고 있습니다. 이는 역까지 소요시간이 늘면 집 가격이 낮아진다라는 사실을 나타내는 것이죠. x축의 소요시간이 늘면 y축 집세가 줄어드는 상관으로 즉 두 변량은 음의 상관관계가 있다고 하는 것입니다. 반대로 두 변량이 모두 늘어나는 경우 산포도는 우상향이 되어 양의 상관관계가 있는 것입니다.
이처럼 두 가지 변량 사이에 어떤 관계성이 보일 때 상관이 있다고 합니다. 특히 직선적 관계에 가까울수록 상관이 강하다고 하고 이를 나타내는 지표가 바로 상관계수 입니다.
상관계수 r
TIP > 상관계수는 영어로 correlation coefficient 입니다. 앞글자가 C 이지만 수학에서 C는 상수(constant)를 뜻하므로 상관계수는 상관(relation)의 앞글자 r 을 사용합니다.
상관계수 r 값으로 상관관계가 양인지 음인지, 직선적 관계에 얼마나 가까운지 알 수 있습니다. r 값이 양수라면 양의 상관관계, 음수라면 음의 상관관계이고 또 r 은 반드시 -1과 1 사이의 값이고 r 이 1이나 -1에 가까울수록 직선적 관계입니다.
위 그림처럼
i) r이 양수(r>0)일 때 우상향 직선관계(양의 상관) -> 1에 가까울 수록 강한 양의 상관관계
ii) r이 음수(r<0)일 때 우하향 직선관계(음의 상관) -> -1에 가까울 수록 강한 음의 상관관계
iii) r이 0에 가까울 때 직선관계 없음 -> 직선관계에서 멀어짐
으로 판단할 수 있습니다.
상관계수, 이것만은 꼭 알아야 합니다.
상관계수는 직접적인 관계에 가까운지를 알아보는 지표
아래와 같이 상관계수 r 값과 상관 기준을 보면 0.0 ~ ±0.3은 거의 상관없음 이지만, 이는 직선적인 관계에 해당합니다. 예를 들어 아래 그림과 같은 곡선형 산포도는 상관계수가 0이지만 어떤 관계성(상관)을 찾을 수 있기 때문에 결국 상관이 있다고 할 수 있어요.
상관계수 r 값과 상관 정도
r=0에 가까운 산포도 값의 예
산포도 위에서 기울기 크기는 상관관계에 영향을 주지 않는다.
아래의 두 산포도는 키와 몸무게 데이터를 예로 든 것입니다. 세로축의 몸무게 단위를 kg에서 g으로 바꾸었기 때문에 직선적인 관계를 보면 기울기에 차이가 있지만 상관계수 r 값은 같습니다.
기울기 정도가 다르게 보이지만 상관계수 r 의 값은 같습니다.
완전상관(r=1, r=-1)이란?
상관계수가 r=1 또는 r=-1일 때 완전상관이라고 합니다. 예를 들어 100원짜리 물건 한 개를 샀을 때 물건 개수와 합계 금액은 r=1이 됩니다.(기울기가 양에 비례합니다) 또 11팀이 겨루는 경기에서 아래 그림처럼 승리와 패배가 직선 모양으로 나열되어 있으면 상관계수 값은 r=-1이 됩니다.
승수와 패수 간 관계
이상 퀵데이터서 데이터 간의 관계성을 산포도와 상관으로 알아보았습니다. 다음에는 상관계수 구하는 방법을 예로 들어 알아볼게요~~^^
"기업 및 공공 데이터 통계적 분석"
"검증되고 수준 높은 설문 기획"
"인포그래픽을 이용한 디자인 보고서"
"석박사 학위 논문 컨설팅"
퀵데이터 함께 합니다!!
(주)한국교육데이터
#상관관계 #상관계수 #산포도 #마케팅조사 #시장조사 #기업설문지 #기관설문지 #설문기획 #서베이 #리서치 #통계분석 #데이터분석 #기업데이터 #정부데이터 #지자체통계 #박사논문 #석사논문 #박사통계분석 #한국교육데이터
'논문 > 논문통계' 카테고리의 다른 글
| 조사목적에 맞는 자료 수집방법. '퀵데이터'에서 '설문지 작성 방법' 알아보기 (0) | 2020.11.12 |
|---|---|
| 통계는 판단 자료의 하나! 퀵데이터에서 허위상관에 대해 알아볼까요? (0) | 2020.09.23 |
| P 값의 'P'는 뭘 까요?? 퀵데이터에서 알아봐요^^ (0) | 2020.08.18 |
| 통계는 왜 필요할까요???_퀵데이터 (0) | 2020.08.18 |
| 통계학의 척도! 데이터 분류 기준은 어떻게 할까요?_퀵데이터 (0) | 2020.08.18 |
